In this article, We'll talk about one of the fundamental concepts in computer science - The Finite Automata. We'll look what exactly it is and understand where can they be used.
What is a Finite Automata?
A one word answer would be - a recognizer. It simply tells whether a string belongs to a language or not.
It is something like asking it, whether the string - अभिलेख belongs to the English Language and it simply replies No.
I'll use the transition diagram to demonstrate how it exactly works.
Transition Diagram Basics
- Every Transition diagram has a starting state and is represented by:
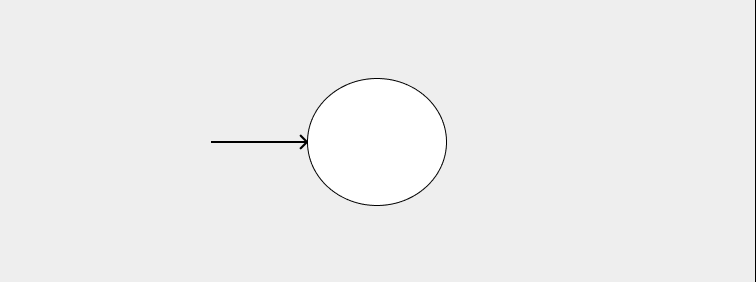
- Every Transition diagram has a final state and is represented by:
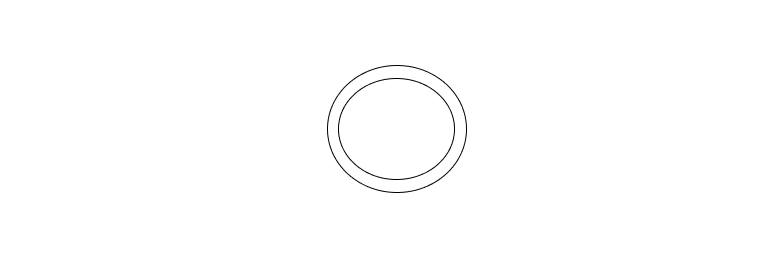
- To indicate that the automata will transition to state
BfromAwhen a symbolais encountered we use:
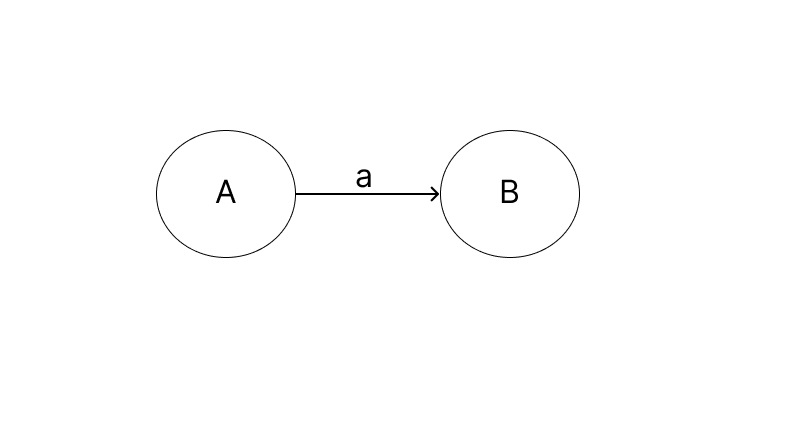
- To indicate that the automata will not transition to another state when a symbol a is encountered we use:
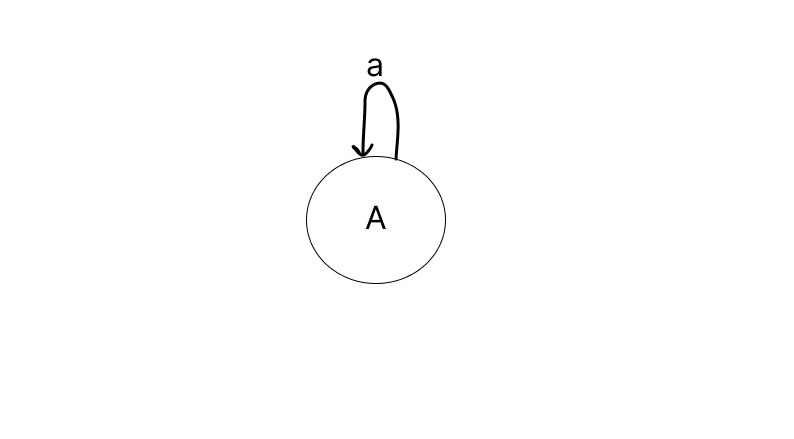
Note: We refer the arrow head in transition diagram as an edge and that 'a' above the edge as a label.
Types of Finite Automata
Finite Automata are of two types:
1. Non-Deterministic Finite Automata (NFA)
Lets see a transition diagram first. Let me just remind you this is not a complete diagram, it is missing a start and end state.
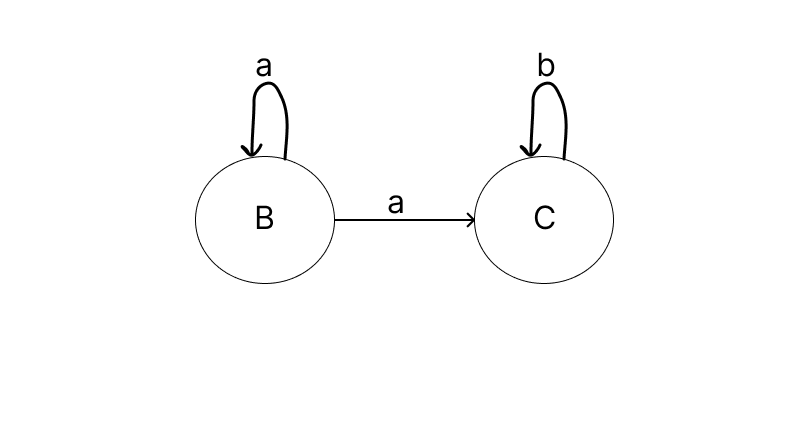
Things to note here:
a. The state B has two edges with the same label a to two different states - C and B itself. This is what non-deterministic means, you cannot tell where the automata will transition to.
b. The state B doesn't care about the symbol b i.e., it has no edge with the label b.
c. The state C also doesn't care about the symbol a, i.e., it has no edge with label a.
d. NFA allows epsilon transition, i.e. you can set transition from one state to another state on empty string as well.
2. Deterministic Finite Automate (DFA)
Lets see a transition diagram first.
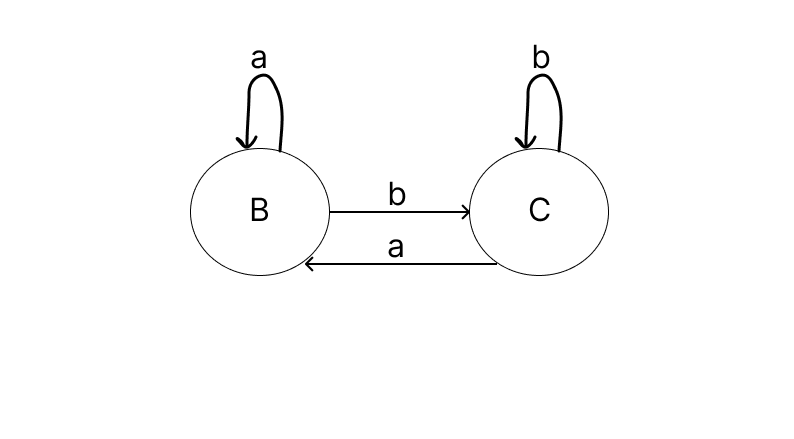
Comparing the above image with the previous image we get the following differences:
a. State B has two edges with different labels. We cannot have multiple edges with same labels from a state in DFA.
b. Both state B and C now care about the symbols b and a respectively. In DFA there must a edge for every symbols in the language from every state.
c. DFA don't allow epsilon transition.
You might have felt, NFA more powerful, but let me tell you that they have the same power and both of them are capable of recognizing the same langauge- Regular Language. It can be proved that they are equivalent but not here, for sure.
Before we dive more into Finite Automata, lets look at some basic fundamental required:
1.Alphabet
Alphabet is a finite, non-empty set whose elements are symbols.
2. String
A string is a sequence of alphabet. It is denoted by w and |w| denotes its length.
3. Concatenation
If x and y are two strings or symbols, then their concatenation xy means, string x followed by string y.
4. OR
OR is generally denoted by a + or |. Notation like x|y means either x or y.
5. Kleen Closure
Kleen Closure, denoted by a *, means one or more occurrence. Notation like (x)* mean one or more occurrence of x.
I think its time to get somewhat formal.
Finite Automata Again
Finite Automata is a model of computation that recognizes regular language. It has finite set of states, edges labelled with symbols that leads to states and a transition function which tells where to transit, on a particluar input symbol.
Basically, we pass in, a string to a finite automate it transits through multiple states according to the transition function, if it reaches the end of the string and it is at the final (end) state, the automata is said to accept the string.
If it reaches the end of the string and it is not at the final state, the automata is said to reject the string (just like how she rejected me!!).
I'll now present you a example of designing a Finite Automate - DFA.
A Finite Automata for Language, that has two symbols - a and b where the number of b's is even.
Thought Process
a. We can start by thinking the strings that belongs to this langauge - a (Since 0 is even and it has even number of b so it must accepted by our automata.), abb, bb, aabb, abbbb etc and try working out with those strings.
b. We should do something, such that we are able to count the number of b's, while we are reading through the string, we should be at the final state whenever the number of b is even.
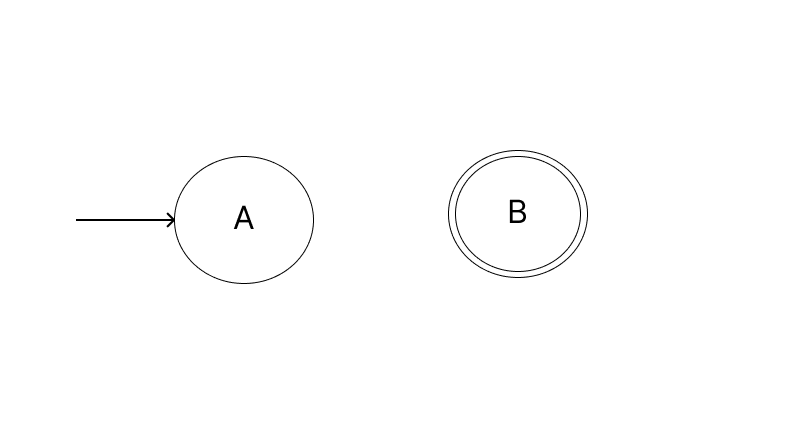
Lets start by assuming that we'll need just two states - A and B. A being both the start state and B the final state.
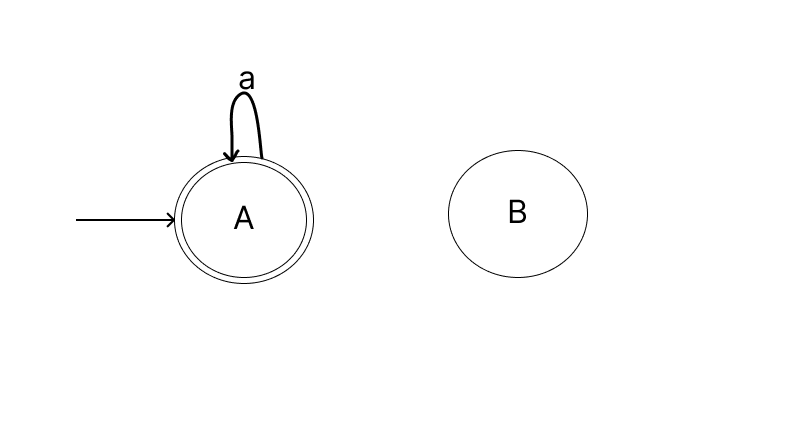
Remember what I said earlier, we have to be at the final state when the number of b is even. So we have to remain at the state A when we get a a because a single a is even b.
Now we need to think of, what to do when we get a b at the state A - The start state. Since a single b should be rejected, we should move to the state B.
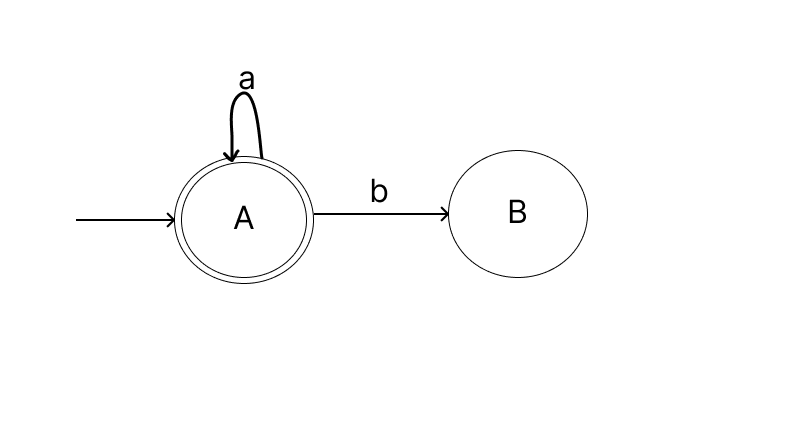
We'll be at state B after we read a b when we are at state A. So when we get another b it's the second b i.e., even number of b's and we have to be at the final state whenever we encounter even b's. So ,
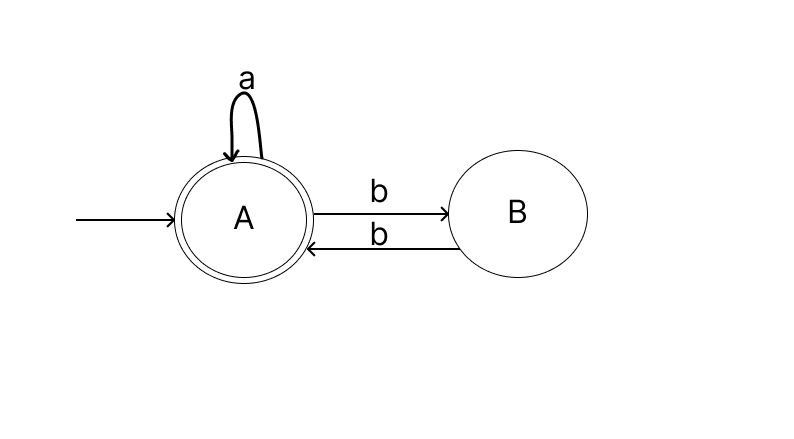
Ok the final question, what to do when we are at state B and we encounter a a? - With the configuration so far we'll be at state B when we have odd number of bs. So no matter how many a's we encounter we need to stay at state B. So,
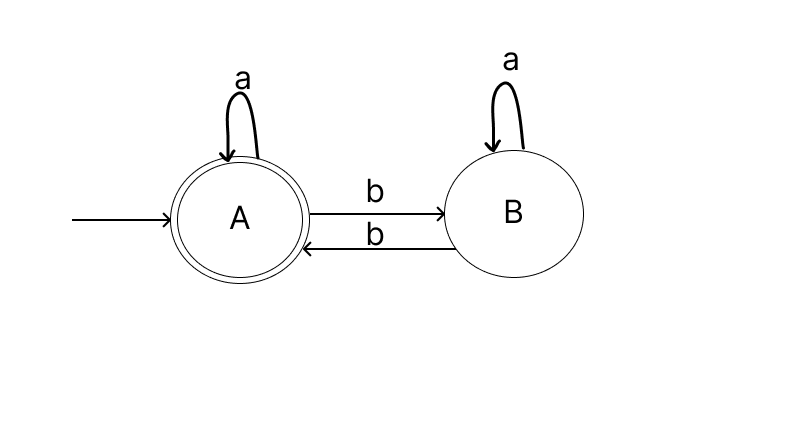
This is it, the final configuration for our DFA.
Now, lets see how we can define the transition function for this DFA.
A transition function takes two inputs - the current state and the input. It outputs the state where the automata should transit to.
So, when we are at the state A and encounter the symbol a we stay at the state A, so we write
TF(A, a) = A
Similarly when we are at state A and encounter the symbol b we move to the state B, so
TF(A, b) = B
Similarly we can write,
TF(B, a) = B
TF(B, b) = A
Usage
- Flex - The Lexical analyzer generator, uses the concept of Finite Automata.
This is it for this article.
Happy Learning!